In this article, I am going to show you the solution of a commonly asked question in programming interviews. This question is the following:
Calculate the sum of two integers a and b, but you are not allowed to use the operators + and -.
This is a typical and a relatively easier question and measures your ability to find a solution without using basic operators. As you see, we are not allowed to use mathematical operators. This forces the programmer to use either a higher level class such as BigInteger or to use a lower level approach, bitwise operations. Now let's have a look at these solutions:
This is a typical and a relatively easier question and measures your ability to find a solution without using basic operators. As you see, we are not allowed to use mathematical operators. This forces the programmer to use either a higher level class such as BigInteger or to use a lower level approach, bitwise operations. Now let's have a look at these solutions:
package other;
import java.math.BigInteger;
public class Solution {
/**
* Summation using bitwise operations
* @param a of type int
* @param b of type int
* @return a
*/
public int getSum(int a, int b) {
int carry = 0;
while (b != 0) {
carry = a & b;
a = a ^ b;
b = carry << 1;
}
return a;
}
/**
* Summation using BigInteger class
* @param a of type int
* @param b of type int
* @return int
*/
public int getSum2(int a, int b) {
BigInteger c = BigInteger.valueOf(a);
BigInteger d = BigInteger.valueOf(b);
return c.add(d).intValue();
}
}
Using Bitwise Operations
The first method getSum(int, int) uses the bitwise operations to calculate the sum of the given two integers. If this looks meaningless to you, let me explain the logic behind it:
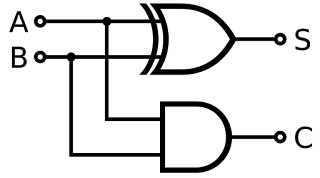
If you know binary arithmetic or how to add numbers in binary format, you may be familiar with the fact that the sum of two numbers can be obtained by using the XOR operation and carry, by using AND operation. Let's see the circuit that represents this operation:
Since we have more than one bits in our integers, we need to use a while loop or any other loops to calculate the sum. Let's say a is 28 and b is 8;
If we convert them to binary:
a = 11100
b = 01000
// First while loop iteration
carry = a&b = 01000
a = a^b = 10100
b = carry << 1 = 10000
// Second while loop iteration
carry = a&b = 10000
a = a^b = 00100
b = carry << 1 = 100000
b = carry << 1 = 100000
carry = a&b = 000000
a = a^b = 100100
b = carry << 1 = 000000
When b is all zeros, the iteration stops; since while(b != 0) and the last value of a is returned:
a= 100100 and it's integer equivalent is 36, which is the summation result!
The second method uses the class called BigInteger which is in the math library in Java. This class is used to deal with greater valued integers but it is also perfectly fine for this question.
Finally, let's give the test cases for these two methods and see if they pass the JUnit tests:
b = carry << 1 = 000000
When b is all zeros, the iteration stops; since while(b != 0) and the last value of a is returned:
a= 100100 and it's integer equivalent is 36, which is the summation result!
Using BigInteger Class
The second method uses the class called BigInteger which is in the math library in Java. This class is used to deal with greater valued integers but it is also perfectly fine for this question.
Results
Finally, let's give the test cases for these two methods and see if they pass the JUnit tests:
package tests;
import static org.junit.Assert.*;
import org.junit.BeforeClass;
import org.junit.Test;
import other.Solution;
public class TestSolution {
static int a, b;
static Solution s;
@BeforeClass
public static void setUpBeforeClass() throws Exception {
a = 5;
b = 10;
s = new Solution();
}
@Test
public void testGetSum() {
assertEquals(s.getSum(a, b), a + b, 0);
}
@Test
public void testGetSum2() {
assertEquals(s.getSum2(a, b), a + b, 0);
}
}
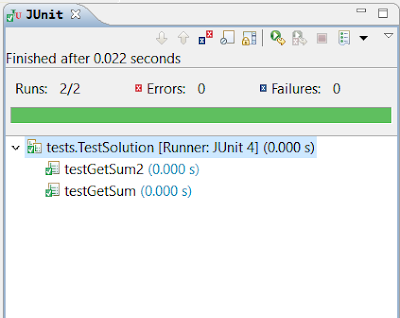
As you can see, both methods passed these unit tests successfully.
Hope this article is helpful, please leave a comment if you have any questions or suggestions. Happy coding!

Disqus Comments Loading..